21 Graphs
In From Acyclicity to Cycles we introduced a special kind of sharing: when the data become cyclic, i.e., there exist values such that traversing other reachable values from them eventually gets you back to the value at which you began. Data that have this characteristic are called graphs.Technically, a cycle is not necessary to be a graph; a tree or a DAG is also regarded as a (degenerate) graph. In this section, however, we are interested in graphs that have the potential for cycles.
Lots of very important data are graphs. For instance, the people and connections in social media form a graph: the people are nodes or vertices and the connections (such as friendships) are links or edges. They form a graph because for many people, if you follow their friends and then the friends of their friends, you will eventually get back to the person you started with. (Most simply, this happens when two people are each others’ friends.) The Web, similarly is a graph: the nodes are pages and the edges are links between pages. The Internet is a graph: the nodes are machines and the edges are links between machines. A transportation network is a graph: e.g., cities are nodes and the edges are transportation links between them. And so on. Therefore, it is essential to understand graphs to represent and process a great deal of interesting real-world data.
Graphs are important and interesting for not only practical but also principled reasons. The property that a traversal can end up where it began means that traditional methods of processing will no longer work: if it blindly processes every node it visits, it could end up in an infinite loop. Therefore, we need better structural recipes for our programs. In addition, graphs have a very rich structure, which lends itself to several interesting computations over them. We will study both these aspects of graphs below.
21.1 Understanding Graphs
data BinT: | leaf | node(v, l :: ( -> BinT), r :: ( -> BinT)) end
rec tr = node("rec", lam(): tr end, lam(): tr end) t0 = node(0, lam(): leaf end, lam(): leaf end) t1 = node(1, lam(): t0 end, lam(): t0 end) t2 = node(2, lam(): t1 end, lam(): t1 end)
fun sizeinf(t :: BinT) -> Number: cases (BinT) t: | leaf => 0 | node(v, l, r) => ls = sizeinf(l()) rs = sizeinf(r()) 1 + ls + rs end end
Do Now!
What happens when we call sizeinf(tr)?
It goes into an infinite loop: hence the inf in its name.
check: size(tr) is 1 size(t0) is 1 size(t1) is 2 size(t2) is 3 end
It’s clear that we need to somehow remember what nodes we have visited previously: that is, we need a computation with “memory”. In principle this is easy: we just create an extra data structure that checks whether a node has already been counted. As long as we update this data structure correctly, we should be all set. Here’s an implementation.
fun sizect(t :: BinT) -> Number: fun szacc(shadow t :: BinT, seen :: List<BinT>) -> Number: if has-id(seen, t): 0 else: cases (BinT) t: | leaf => 0 | node(v, l, r) => ns = link(t, seen) ls = szacc(l(), ns) rs = szacc(r(), ns) 1 + ls + rs end end end szacc(t, empty) end
fun has-id<A>(seen :: List<A>, t :: A): cases (List) seen: | empty => false | link(f, r) => if f <=> t: true else: has-id(r, t) end end end
How does this do? Well, sizect(tr) is indeed 1, but sizect(t1) is 3 and sizect(t2) is 7!
Do Now!
Explain why these answers came out as they did.
ls = szacc(l(), ns) rs = szacc(r(), ns)
The remedy for this, therefore, is to remember every node we
visit. Then, when we have no more nodes to process, instead of
returning only the size, we should return all the nodes visited
until now. This ensures that nodes that have multiple paths to them
are visited on only one path, not more than once. The logic for this
is to return two values from each traversal—
fun size(t :: BinT) -> Number: fun szacc(shadow t :: BinT, seen :: List<BinT>) -> {n :: Number, s :: List<BinT>}: if has-id(seen, t): {n: 0, s: seen} else: cases (BinT) t: | leaf => {n: 0, s: seen} | node(v, l, r) => ns = link(t, seen) ls = szacc(l(), ns) rs = szacc(r(), ls.s) {n: 1 + ls.n + rs.n, s: rs.s} end end end szacc(t, empty).n end
Sure enough, this function satisfies the above tests.
21.2 Representations
The representation we’ve seen above for graphs is certainly a start towards creating cyclic data, but it’s not very elegant. It’s both error-prone and inelegant to have to write lam everywhere, and remember to apply functions to () to obtain the actual values. Therefore, here we explore other representations of graphs that are more conventional and also much simpler to manipulate.
The structure of the graph, and in particular, its density. We will discuss this further later [Measuring Complexity for Graphs].
The representation in which the data are provided by external sources. Sometimes it may be easier to simply adapt to their representation; in particular, in some cases there may not even be a choice.
The features provided by the programming language, which make some representations much harder to use than others.
A way to construct graphs.
A way to identify (i.e., tell apart) nodes or vertices in a graph.
Given a way to identify nodes, a way to get that node’s neighbors in the graph.
Our running example will be a graph whose nodes are cities in the United States and edges are direct flight connections between them:
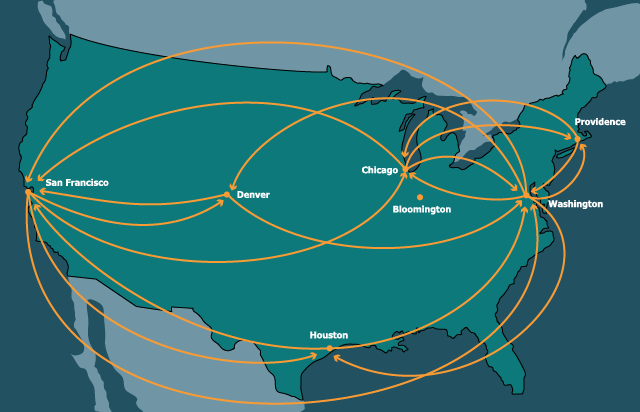
21.2.1 Links by Name
type Key = String data KeyedNode: | keyed-node(key :: Key, content, adj :: List<String>) end type KNGraph = List<KeyedNode> type Node = KeyedNode type Graph = KNGraph
kn-cities :: Graph = block: knWAS = keyed-node("was", "Washington", [list: "chi", "den", "saf", "hou", "pvd"]) knORD = keyed-node("chi", "Chicago", [list: "was", "saf", "pvd"]) knBLM = keyed-node("bmg", "Bloomington", [list: ]) knHOU = keyed-node("hou", "Houston", [list: "was", "saf"]) knDEN = keyed-node("den", "Denver", [list: "was", "saf"]) knSFO = keyed-node("saf", "San Francisco", [list: "was", "den", "chi", "hou"]) knPVD = keyed-node("pvd", "Providence", [list: "was", "chi"]) [list: knWAS, knORD, knBLM, knHOU, knDEN, knSFO, knPVD] end
fun find-kn(key :: Key, graph :: Graph) -> Node: matches = for filter(n from graph): n.key == key end matches.first # there had better be exactly one! end
Exercise
Convert the comment in the function into an invariant about the datum. Express this invariant as a refinement and add it to the declaration of graphs.
fun kn-neighbors(city :: Key, graph :: Graph) -> List<Key>: city-node = find-kn(city, graph) city-node.adj end
check: ns = kn-neighbors("hou", kn-cities) ns is [list: "was", "saf"] map(_.content, map(find-kn(_, kn-cities), ns)) is [list: "Washington", "San Francisco"] end
21.2.2 Links by Indices
In some languages, it is common to use numbers as names. This is
especially useful when numbers can be used to get access to an element
in a constant amount of time (in return for having a bound on the
number of elements that can be accessed). Here, we use a list—
data IndexedNode: | idxed-node(content, adj :: List<Number>) end type IXGraph = List<IndexedNode> type Node = IndexedNode type Graph = IXGraph
ix-cities :: Graph = block: inWAS = idxed-node("Washington", [list: 1, 4, 5, 3, 6]) inORD = idxed-node("Chicago", [list: 0, 5, 6]) inBLM = idxed-node("Bloomington", [list: ]) inHOU = idxed-node("Houston", [list: 0, 5]) inDEN = idxed-node("Denver", [list: 0, 5]) inSFO = idxed-node("San Francisco", [list: 0, 4, 3]) inPVD = idxed-node("Providence", [list: 0, 1]) [list: inWAS, inORD, inBLM, inHOU, inDEN, inSFO, inPVD] end
fun find-ix(idx :: Key, graph :: Graph) -> Node: lists.get(graph, idx) end
fun ix-neighbors(city :: Key, graph :: Graph) -> List<Key>: city-node = find-ix(city, graph) city-node.adj end
check: ns = ix-neighbors(3, ix-cities) ns is [list: 0, 5] map(_.content, map(find-ix(_, ix-cities), ns)) is [list: "Washington", "San Francisco"] end
Something deeper is going on here. The keyed nodes have intrinsic keys: the key is part of the datum itself. Thus, given just a node, we can determine its key. In contrast, the indexed nodes represent extrinsic keys: the keys are determined outside the datum, and in particular by the position in some other data structure. Given a node and not the entire graph, we cannot know for what its key is. Even given the entire graph, we can only determine its key by using identical, which is a rather unsatisfactory approach to recovering fundamental information. This highlights a weakness of using extrinsically keyed representations of information. (In return, extrinsically keyed representations are easier to reassemble into new collections of data, because there is no danger of keys clashing: there are no intrinsic keys to clash.)
21.2.3 A List of Edges
data Edge: | edge(src :: String, dst :: String) end type LEGraph = List<Edge> type Graph = LEGraph
le-cities :: Graph = [list: edge("Washington", "Chicago"), edge("Washington", "Denver"), edge("Washington", "San Francisco"), edge("Washington", "Houston"), edge("Washington", "Providence"), edge("Chicago", "Washington"), edge("Chicago", "San Francisco"), edge("Chicago", "Providence"), edge("Houston", "Washington"), edge("Houston", "San Francisco"), edge("Denver", "Washington"), edge("Denver", "San Francisco"), edge("San Francisco", "Washington"), edge("San Francisco", "Denver"), edge("San Francisco", "Houston"), edge("Providence", "Washington"), edge("Providence", "Chicago") ]
fun le-neighbors(city :: Key, graph :: Graph) -> List<Key>: neighboring-edges = for filter(e from graph): city == e.src end names = for map(e from neighboring-edges): e.dst end names end
check: le-neighbors("Houston", le-cities) is [list: "Washington", "San Francisco"] end
21.2.4 Abstracting Representations
We would like a general representation that lets us abstract over the
specific implementations. We will assume that broadly we have
available a notion of Node that has content, a notion of
Keys (whether or not intrinsic), and a way to obtain the
neighbors—
21.3 Measuring Complexity for Graphs
Before we begin to define algorithms over graphs, we should consider how to measure the size of a graph. A graph has two components: its nodes and its edges. Some algorithms are going to focus on nodes (e.g., visiting each of them), while others will focus on edges, and some will care about both. So which do we use as the basis for counting operations: nodes or edges?
No two nodes are connected. Then there are no edges at all.
Every two nodes is connected. Then there are essentially as many edges as the number of pairs of nodes.
Therefore, when we want to speak of the complexity of algorithms over graphs, we have to consider the sizes of both the number of nodes and edges. In a connected graphA graph is connected if, from every node, we can traverse edges to get to every other node., however, there must be at least as many edges as nodes, which means the number of edges dominates the number of nodes. Since we are usually processing connected graphs, or connected parts of graphs one at a time, we can bound the number of nodes by the number of edges.
21.4 Reachability
Many uses of graphs need to address reachability: whether we can, using edges in the graph, get from one node to another. For instance, a social network might suggest as contacts all those who are reachable from existing contacts. On the Internet, traffic engineers care about whether packets can get from one machine to another. On the Web, we care about whether all public pages on a site are reachable from the home page. We will study how to compute reachability using our travel graph as a running example.
21.4.1 Simple Recursion
If they are the same, then clearly reachability is trivially satisfied.
If they are not, we have to iterate through the neighbors of the source node and ask whether the destination is reachable from each of those neighbors.
fun reach-1(src :: Key, dst :: Key, g :: Graph) -> Boolean: |
if src == dst: |
true |
else: |
loop(neighbors(src, g)) |
end |
end |
fun loop(ns): |
cases (List) ns: |
| empty => false |
| link(f, r) => |
if reach-1(f, dst, g): true else: loop(r) end |
end |
end |
check: |
reach = reach-1 |
reach("was", "was", kn-cities) is true |
reach("was", "chi", kn-cities) is true |
reach("was", "bmg", kn-cities) is false |
reach("was", "hou", kn-cities) is true |
reach("was", "den", kn-cities) is true |
reach("was", "saf", kn-cities) is true |
end |
Exercise
Which of the above examples leads to a cycle? Why?
21.4.2 Cleaning up the Loop
Before we continue, let’s try to improve the expression of the loop. While the nested function above is a perfectly reasonable definition, we can use Pyret’s for to improve its readability.
fun ormap(fun-body, l): cases (List) l: | empty => false | link(f, r) => if fun-body(f): true else: ormap(fun-body, r) end end end
for ormap(n from neighbors(src, g)): reach-1(n, dst, g) end
21.4.3 Traversal with Memory
Because we have cyclic data, we have to remember what nodes we’ve already visited and avoid traversing them again. Then, every time we begin traversing a new node, we add it to the set of nodes we’ve already started to visit so that. If we return to that node, because we can assume the graph has not changed in the meanwhile, we know that additional traversals from that node won’t make any difference to the outcome.This property is known as ☛ idempotence.
fun reach-2(src :: Key, dst :: Key, g :: Graph, visited :: List<Key>) -> Boolean: |
if visited.member(src): |
false |
else if src == dst: |
true |
else: |
new-visited = link(src, visited) |
for ormap(n from neighbors(src, g)): |
reach-2(n, dst, g, new-visited) |
end |
end |
end |
Exercise
Does it matter if the first two conditions were swapped, i.e., the beginning of reach-2 began withif src == dst: true else if visited.member(src): false
? Explain concretely with examples.
Exercise
We repeatedly talk about remembering the nodes that we have begun to visit, not the ones we’ve finished visiting. Does this distinction matter? How?
21.4.4 A Better Interface
fun reach-3(s :: Key, d :: Key, g :: Graph) -> Boolean: fun reacher(src :: Key, dst :: Key, visited :: List<Key>) -> Boolean: if visited.member(src): false else if src == dst: true else: new-visited = link(src, visited) for ormap(n from neighbors(src, g)): reacher(n, dst, new-visited) end end end reacher(s, d, empty) end
Exercise
Does this really gives us a correct implementation? In particular, does this address the problem that the size function above addressed? Create a test case that demonstrates the problem, and then fix it.
21.5 Depth- and Breadth-First Traversals
It is conventional for computer science texts to call these depth- and breadth-first search. However, searching is just a specific purpose; traversal is a general task that can be used for many purposes.
The reachability algorithm we have seen above has a special property. At every node it visits, there is usually a set of adjacent nodes at which it can continue the traversal. It has at least two choices: it can either visit each immediate neighbor first, then visit all of the neighbors’ neighbors; or it can choose a neighbor, recur, and visit the next immediate neighbor only after that visit is done. The former is known as breadth-first traversal, while the latter is depth-first traversal.
The algorithm we have designed uses a depth-first strategy: inside <graph-reach-1-loop>, we recur on the first element of the list of neighbors before we visit the second neighbor, and so on. The alternative would be to have a data structure into which we insert all the neighbors, then pull out an element at a time such that we first visit all the neighbors before their neighbors, and so on. This naturally corresponds to a queue [An Example: Queues from Lists].
Exercise
Using a queue, implement breadth-first traversal.
If we correctly check to ensure we don’t re-visit nodes, then both
breadth- and depth-first traversal will properly visit the entire
reachable graph without repetition (and hence not get into an infinite
loop). Each one traverses from a node only once, from which it
considers every single edge. Thus, if a graph has \(N\) nodes and
\(E\) edges, then a lower-bound on the complexity of traversal is
\(O([N, E \rightarrow N + E])\). We must also consider the cost of checking whether we
have already visited a node before (which is a set membership problem,
which we address elsewhere: Making Sets Grow on Trees). Finally, we have to
consider the cost of maintaining the data structure that keeps track
of our traversal. In the case of depth-first traversal,
recursion—
This would suggest that depth-first traversal is always better than breadth-first traversal. However, breadth-first traversal has one very important and valuable property. Starting from a node \(N\), when it visits a node \(P\), count the number of edges taken to get to \(P\). Breadth-first traversal guarantees that there cannot have been a shorter path to \(P\): that is, it finds a shortest path to \(P\).
Exercise
Why “a” rather than “the” shortest path?
Do Now!
Prove that breadth-first traversal finds a shortest path.
21.6 Graphs With Weighted Edges
Consider a transportation graph: we are usually interested not only in whether we can get from one place to another, but also in what it “costs” (where we may have many different cost measures: money, distance, time, units of carbon dioxide, etc.). On the Internet, we might care about the ☛ latency or ☛ bandwidth over a link. Even in a social network, we might like to describe the degree of closeness of a friend. In short, in many graphs we are interested not only in the direction of an edge but also in some abstract numeric measure, which we call its weight.
In the rest of this study, we will assume that our graph edges have weights. This does not invalidate what we’ve studied so far: if a node is reachable in an unweighted graph, it remains reachable in a weighted one. But the operations we are going to study below only make sense in a weighted graph.We can, however, always treat an unweighted graph as a weighted one by giving every edge the same, constant, positive weight (say one).
Exercise
When treating an unweighted graph as a weighted one, why do we care that every edge be given a positive weight?
Exercise
Revise the graph data definitions to account for edge weights.
Exercise
Weights are not the only kind of data we might record about edges. For instance, if the nodes in a graph represent people, the edges might be labeled with their relationship (“mother”, “friend”, etc.). What other kinds of data can you imagine recording for edges?
21.7 Shortest (or Lightest) Paths
Imagine planning a trip: it’s natural that you might want to get to your destination in the least time, or for the least money, or some other criterion that involves minimizing the sum of edge weights. This is known as computing the shortest path.
We should immediately clarify an unfortunate terminological
confusion. What we really want to compute is the lightest
path—
Exercise
Construct a graph and select a pair of nodes in it such that the shortest path from one to the other is not the lightest one, and vice versa.
We have already seen [Depth- and Breadth-First Traversals] that breadth-first search constructs shortest paths in unweighted graphs. These correspond to lightest paths when there are no weights (or, equivalently, all weights are identical and positive). Now we have to generalize this to the case where the edges have weights.
w :: Key -> Number
w :: Key -> Option<Number>
Now let’s think about this inductively. What do we know initially?
Well, certainly that the source node is at a distance of zero from
itself (that must be the lightest path, because we can’t get any
lighter). This gives us a (trivial) set of nodes for which we already
know the lightest weight. Our goal is to grow this set of
nodes—
Inductively, at each step we have the set of all nodes for which we know the lightest path (initially this is just the source node, but it does mean this set is never empty, which will matter in what we say next). Now consider all the edges adjacent to this set of nodes that lead to nodes for which we don’t already know the lightest path. Choose a node, \(q\), that minimizes the total weight of the path to it. We claim that this will in fact be the lightest path to that node.
If this claim is true, then we are done. That’s because we would now add \(q\) to the set of nodes whose lightest weights we now know, and repeat the process of finding lightest outgoing edges from there. This process has thus added one more node. At some point we will find that there are no edges that lead outside the known set, at which point we can terminate.
It stands to reason that terminating at this point is safe: it corresponds to having computed the reachable set. The only thing left is to demonstrate that this greedy algorithm yields a lightest path to each node.
We will prove this by contradiction. Suppose we have the path \(s \rightarrow d\) from source \(s\) to node \(d\), as found by the algorithm above, but assume also that we have a different path that is actually lighter. At every node, when we added a node along the \(s \rightarrow d\) path, the algorithm would have added a lighter path if it existed. The fact that it did not falsifies our claim that a lighter path exists (there could be a different path of the same weight; this would be permitted by the algorithm, but it also doesn’t contradict our claim). Therefore the algorithm does indeed find the lightest path.
What remains is to determine a data structure that enables this algorithm. At every node, we want to know the least weight from the set of nodes for which we know the least weight to all their neighbors. We could achieve this by sorting, but this is overkill: we don’t actually need a total ordering on all these weights, only the lightest one. A heap [REF] gives us this.
Exercise
What if we allowed edges of weight zero? What would change in the above algorithm?
Exercise
What if we allowed edges of negative weight? What would change in the above algorithm?
For your reference, this algorithm is known as Dijkstra’s Algorithm.
21.8 Moravian Spanning Trees
At the turn of the milennium, the US National Academy of Engineering surveyed its members to determine the “Greatest Engineering Achievements of the 20th Century”. The list contained the usual suspects: electronics, computers, the Internet, and so on. But a perhaps surprising idea topped the list: (rural) electrification.Read more about it on their site.
21.8.1 The Problem
To understand the history of national electrical grids, it helps to go back to Moravia in the 1920s. Like many parts of the world, it was beginning to realize the benefits of electricity and intended to spread it around the region. A Moravian academia named Otakar Borůvka heard about the problem, and in a remarkable effort, described the problem abstractly, so that it could be understood without reference to Moravia or electrical networks. He modeled it as a problem about graphs.
The electrical network must reach all the towns intended to be covered by it. In graph terms, the solution must be spanning, meaning it must visit every node in the graph.
Redundancy is a valuable property in any network: that way, if one set of links goes down, there might be another way to get a payload to its destination. When starting out, however, redundancy may be too expensive, especially if it comes at the cost of not giving someone a payload at all. Thus, the initial solution was best set up without loops or even redundant paths. In graph terms, the solution had to be a tree.
Finally, the goal was to solve this problem for the least cost possible. In graph terms, the graph would be weighted, and the solution had to be a minimum.
21.8.2 A Greedy Solution
Begin with a solution consisting of a single node, chosen arbitrarily. For the graph consisting of this one node, this solution is clearly a minimum, spanning, and a tree.
Of all the edges incident on nodes in the solution that connect to a node not already in the solution, pick the edge with the least weight.Note that we consider only the incident edges, not their weight added to the weight of the node to which they are incident.
Add this edge to the solution. The claim is that for the new solution will be a tree (by construction), spanning (also by construction), and a minimum. The minimality follows by an argument similar to that used for Dijkstra’s Algorithm.
Jarník had the misfortune of publishing this work in Czech in 1930, and it went largely ignored. It was rediscovered by others, most notably by R.C. Prim in 1957, and is now generally known as Prim’s Algorithm, though calling it Jarník’s Algorithm would attribute credit in the right place.
Implementing this algorithm is pretty easy. At each point, we need to know the lightest edge incident on the current solution tree. Finding the lightest edge takes time linear in the number of these edges, but the very lightest one may create a cycle. We therefore need to efficiently check for whether adding an edge would create a cycle, a problem we will return to multiple times [Checking Component Connectedness]. Assuming we can do that effectively, we then want to add the lightest edge and iterate. Even given an efficient solution for checking cyclicity, this would seem to require an operation linear in the number of edges for each node. With better representations we can improve on this complexity, but let’s look at other ideas first.
21.8.3 Another Greedy Solution
Recall that Jarník presented his algorithm in 1930, when computers didn’t exist, and Prim his in 1957, when they were very much in their infancy. Programming computers to track heaps was a non-trivial problem, and many algorithms were implemented by hand, where keeping track of a complex data structure without making errors was harder still. There was need for a solution that was required less manual bookkeeping (literally speaking).
In 1956, Joseph Kruskal presented such a solution. His idea was elegantly simple. The Jarník algorithm suffers from the problem that each time the tree grows, we have to revise the content of the heap, which is already a messy structure to track. Kruskal noted the following.
To obtain a minimum solution, surely we want to include one of the edges of least weight in the graph. Because if not, we can take an otherwise minimal solution, add this edge, and remove one other edge; the graph would still be just as connected, but the overall weight would be no more and, if the removed edge were heavier, would be less.Note the careful wording: there may be many edges of the same least weight, so adding one of them may remove another, and therefore not produce a lighter tree; but the key point is that it certainly will not produce a heavier one. By the same argument we can add the next lightest edge, and the next lightest, and so on. The only time we cannot add the next lightest edge is when it would create a cycle (that problem again!).
Therefore, Kruskal’s algorithm is utterly straightforward. We first
sort all the edges, ordered by ascending weight. We then take each
edge in ascending weight order and add it to the solution provided it
will not create a cycle. When we have thus processed all the edges, we
will have a solution that is a tree (by construction), spanning
(because every connected vertex must be the endpoint of some edge),
and of minimum weight (by the argument above). The complexity is that
of sorting (which is \([e \rightarrow e \log e]\) where \(e\) is the
size of the edge set. We then iterate over each element in \(e\),
which takes time linear in the size of that set—
21.8.4 A Third Solution
Both the Jarník and Kruskal solutions have one flaw: they require a
centralized data structure (the priority heap, or the sorted list) to
incrementally build the solution. As parallel computers became
available, and graph problems grew large, computer scientists looked
for solutions that could be implemented more efficiently in
parallel—
In 1965, M. Sollin constructed an algorithm that met these needs beautifully. In this algorithm, instead of constructing a single solution, we grow multiple solution components (potentially in parallel if we so wish). Each node starts out as a solution component (as it was at the first step of Jarník’s Algorithm). Each node considers the edges incident to it, and picks the lightest one that connects to a different component (that problem again!). If such an edge can be found, the edge becomes part of the solution, and the two components combine to become a single component. The entire process repeats.
Because every node begins as part of the solution, this algorithm naturally spans. Because it checks for cycles and avoids them, it naturally forms a tree.Note that avoiding cycles yields a DAG and is not automatically guaranteed to yield a tree. We have been a bit lax about this difference throughout this section. Finally, minimality follows through similar reasoning as we used in the case of Jarník’s Algorithm, which we have essentially run in parallel, once from each node, until the parallel solution components join up to produce a global solution.
Of course, maintaining the data for this algorithm by hand is a nightmare. Therefore, it would be no surprise that this algorithm was coined in the digital age. The real surprise, therefore, is that it was not: it was originally created by Otakar Borůvka himself.
pinpointed the real problem lying underneath the electrification problem so it could be viewed in a context-independent way,
created a descriptive language of graph theory to define it precisely, and
even solved the problem in addition to defining it.
As you might have guessed by now, this problem is indeed called the MST in other textbooks, but “M” stands not for Moravia but for “Minimum”. But given Borůvka’s forgotten place in history, we prefer the more whimsical name.
21.8.5 Checking Component Connectedness
As we’ve seen, we need to be able to efficiently tell whether two
nodes are in the same component. One way to do this is to conduct a
depth-first traversal (or breadth-first traversal) starting from the
first node and checking whether we ever visit the second one. (Using
one of these traversal strategies ensures that we terminate in the
presence of loops.) Unfortunately, this takes a linear amount of time
(in the size of the graph) for every pair of nodes—
It is helpful to reduce this problem from graph connectivity to a more general one: of disjoint-set structure (colloquially known as union-find for reasons that will soon be clear). If we think of each connected component as a set, then we’re asking whether two nodes are in the same set. But casting it as a set membership problem makes it applicable in several other applications as well.
The setup is as follows. For arbitrary values, we want the ability to think of them as elements in a set. We are interested in two operations. One is obviously union, which merges two sets into one. The other would seem to be something like is-in-same-set that takes two elements and determines whether they’re in the same set. Over time, however, it has proven useful to instead define the operator find that, given an element, “names” the set (more on this in a moment) that the element belongs to. To check whether two elements are in the same set, we then have to get the “set name” for each element, and check whether these names are the same. This certainly sounds more roundabout, but this means we have a primitive that may be useful in other contexts, and from which we can easily implement is-in-same-set.
data Element<T>: | elt(val :: T, parent :: Option<Element>) end
fun is-same-element(e1, e2): e1.val <=> e2.val end
Do Now!
Why do we check only the value parts?
fun is-in-same-set(e1 :: Element, e2 :: Element, s :: Sets) -> Boolean: s1 = fynd(e1, s) s2 = fynd(e2, s) identical(s1, s2) end
type Sets = List<Element>
fun fynd(e :: Element, s :: Sets) -> Element: cases (List) s: | empty => raise("fynd: shouldn't have gotten here") | link(f, r) => if is-same-element(f, e): cases (Option) f.parent: | none => f | some(p) => fynd(p, s) end else: fynd(e, r) end end end
Exercise
Why is there a recursive call in the nested cases?
fun union(e1 :: Element, e2 :: Element, s :: Sets) -> Sets: s1 = fynd(e1, s) s2 = fynd(e2, s) if identical(s1, s2): s else: update-set-with(s, s1, s2) end end
fun update-set-with(s :: Sets, child :: Element, parent :: Element) -> Sets: cases (List) s: | empty => raise("update: shouldn't have gotten here") | link(f, r) => if is-same-element(f, child): link(elt(f.val, some(parent)), r) else: link(f, update-set-with(r, child, parent)) end end end
check: s0 = map(elt(_, none), [list: 0, 1, 2, 3, 4, 5, 6, 7]) s1 = union(index(s0, 0), index(s0, 2), s0) s2 = union(index(s1, 0), index(s1, 3), s1) s3 = union(index(s2, 3), index(s2, 5), s2) print(s3) is-same-element(fynd(index(s0, 0), s3), fynd(index(s0, 5), s3)) is true is-same-element(fynd(index(s0, 2), s3), fynd(index(s0, 5), s3)) is true is-same-element(fynd(index(s0, 3), s3), fynd(index(s0, 5), s3)) is true is-same-element(fynd(index(s0, 5), s3), fynd(index(s0, 5), s3)) is true is-same-element(fynd(index(s0, 7), s3), fynd(index(s0, 7), s3)) is true end
First, because we are performing functional updates, the value of the parent reference keeps “changing”, but these changes are not visible to older copies of the “same” value. An element from different stages of unioning has different parent references, even though it is arguably the same element throughout. This is a place where functional programming hurts.
Relatedly, the performance of this implementation is quite bad. fynd recursively traverses parents to find the set’s name, but the elements traversed are not updated to record this new name. We certainly could update them by reconstructing the set afresh each time, but that complicates the implementation and, as we will soon see, we can do much better.